Complex Analysis for physicists (5) - 복소적분

이 글은 2019.12.06에 작성됨.

원본 : physvillain.blogspot.com/2019/12/complex-analysis-for-physicists-5.html

 

내용이 많아 크게 두 가지로 나눈다. 다소 필수적인 내용을 [ PART I ]에서, 다소 부수적이고 어려울 수 있는 내용을 [ PART II ]에서 다룬다.

[ PART I ]

복소함수의 적분은 정의역이 $\mathbb{C}$이므로 적분영역이 2차원, 즉 경로적분이다. 또, 해석함수의 여러 특징들로부터 2차원 벡터장의 미적분으로 생각할 수도 있으며 $(0,1)^2=(-1,0)$이라는 규칙이 주는 특이한 성질도 있을 것이다. 우리는 주로 $\mathbb{C}$내부의 닫힌 경로 $C$에 대한 적분을 수행할 것이고, 적분 적분하는 영역을 매개변수화 한다면 $f(z) dz = f(z(t))z'(t)dt$와 같이 표현하여 그냥 미적분학에서 스칼라장을 선적분하는 것처럼 계산하면 된다. 적분 테크닉적인 부분은 미적분학에서 했던것과 동일하니 넘어가고, 꼭 필요한 개념만 짚어보도록 하자. 어떤 복소함수 $f=u+iv$가 어떤 simple-connected $D$에서 analytic하다면 D에서 부정적분 $F=U+iV$이 존재하는데, (뒤에서 볼 것임) 이 부정적분 역시 analytic이다. 그래서 $f$의 부정적분 $F$도 Cauchy-Riemann $\vec{\nabla}\times \vec{\bar{F}} = \vec{0}$, $\vec{\nabla}\cdot\vec{\bar{F}}=0$를 만족하는데, 이것 때문에 적분경로$C$가 $C \in D$라면 다음이 성립한다.
$$\int_C (u+iv)(dx+idy) = \int_C (udx-vdy)+i(vdx+udy) \\ = \int_C (\partial_x U dx + \partial_y U dy)+i(\partial_x V dx+ \partial_y dy) = \int_{F(C)} dU+idV = 0$$
이것은 무엇을 상징하는가? 내부가 해석적이면 내부의 어떤 닫힌경로를 잡든 적분결과는 0이다. 이것이 Cauchy-Goursat thm이다. 우리는 부정적분의 존재성과 해석적임을 기반으로 이것을 증명한 것인데, 이것을 요구하지 않는 증명이 존재한다. Cauchy는 $f'(z)$의 연속성을 가정하고 증명에 성공하였고, 후에 Edouard Goursat이 $f'(z)$의 연속성을 요구하지 않는 증명을 완성했다. 증명은 꽤나 복잡하므로 생략할 것이고(나는 관심도 없고), 다음을 정리마냥 받아들이고 사용할 것이다. 

THM 5-1 : Cauchy-Goursat thm

$f$ is analytic in simple-connected $D$. Then for all simple-closed path $C\in D$, $\int_C f(z) dz=0$

이것의 역으로 Morera's thm이라는 것이 존재한다. 그 내용은 말 그대로 $D$안의 모든 closed path C에 대해서 $\int_C f(z)dz=0$이라면 $f$가 $D$에서 해석적이라는 것이다. 그리고 이 정리들을 받아들일 수 있다면, 부정적분의 존재성과 미적분학의 기본정리 역시 증명가능하다.

THM 5-2 : 부정적분의 존재성과 미적분학의 기본정리

$f$ is analytic in simple-connected $D$, and $z_0$ is fixed point in $D$. For any path from $z_0$ to $z$,

$$F(z)=\int_C f(z')dz'=\int_{z_0}^{z} f(z')dz'$$

is well-defined in $D$ and $F'(z)=f(z)$. And for fixed pt $z_1 \in C$, 

$$\int_C f(z) dz = F(z_1)-F(z_0)$$

 

이것의 증명은 Cauchy-Goursat thm으로부터 꽤나 간단하게 증명이 가능하나 역시 증명은 생략한다. 대충 받아들이기 쉽게 설명하자면, 애초에 Cauchy-Riemann이 주는 조건 자체가 보존장에서의 경로독립성을 이야기 해준다. Curl이 0이므로 미적분학에서처럼 원시함수가 존재할 것 같지 않은가? 또, 반대로 부정적분이 존재하므로 도함수도 존재할 것 같지 않은 느낌이 들 것이다. 실제로 $D$에서 analytic이면 그것의 모든 도함수가 존재한다.(증명은 생략할 것이다.) 미분가능하므로 도함수의 연속성도 보장이 될 것이고 따라서 $D$에서 조화인 함수 $u$를 어떤 복소함수의 실/허수부로 보면 그것의 모든 편도함수들 $\partial_j u$, $\partial_j \partial_l u$가 존재하며 모두 조화함수이다. 다음의 공식은 모든 도함수에 대한 공식을 제공한다.

THM 5-3 : Cauchy Integral Formula

$f$ is analytic in simple-connected $D$. Then for all simple-closed path $C\in D$ and for all $z_0 \in \int C$,

$$f^{(n)}(z_0)=\frac{n!}{i2\pi} \int_C \frac{f(z)}{(z-z_0)^{n+1}} dz$$

 

우선 $n=0$일 때 증명해보자. 간단한 계산으로부터 $\int_{C_1(z_0)} \frac{dz}{z-z_0}=i2\pi$임을 보일 수 있고, 경로독립성과 Cauchy-Goursat thm을 잘 이용하면 $z_0$을 포함하는 아무런 $C$에 대하여 $\int_C \frac{dz}{z-z_0}=i2\pi$임을 보일 수 있다.
$$\left| \frac{1}{i2\pi} \int_C \frac{f(z)dz}{z-z_0}-f(z_0) \right|=\left| \frac{1}{i2\pi} \int_{C_\epsilon(z_0)} \frac{f(z)}{z-z_0}dz - \frac{1}{i2\pi} \int_{C_\epsilon(z_0)} \frac{f(z_0)}{z-z_0}dz \right| \\ \leq \frac{1}{2\pi} \int_{C_\epsilon(z_0)} \frac{|f(z)-f(z_0)|}{|z-z_0|}|dz| \leq \frac{1}{2\pi} \frac{\epsilon}{\delta} 2\pi \delta=\epsilon$$
이것을 이제 $z_0$에 대해 n번 편미분하면 증명된다.

다음으로 해석함수의 두 가지 대표적인 성질 때문에 나타나는 것을 보자. 우리는 전자기학에서 harmonic function의 특징들을 살펴본 적 있다. n차원 Laplace-eq를 만족하는 해를 $u$라 하면 n차원 구 표면에 대한 $u$의 평균값은 구 중심에서의 함수값 $u(\vec{r}_{center})$와 같음을 알 것이다.
$$u(\vec{r}_{center})=\frac{\int u(\vec{r}) d\Omega_n}{\int d\Omega_n}$$
이것의 2차원 특수케이스에서
$$u(\vec{r}_{center})=\frac{1}{2\pi} \int u(x_c+R\cos \theta,y_c+R\sin \theta) d\theta$$
analytic function $f=u+iv$라 하면, $v$ 역시 harmonic이므로 위의 식을 만족할 것이다. $v$에 대한 식에 $i$를 곱하고 더하면 따라서 다음의 정리가 증명된다.

THM 5-4 : Gauss Mean-value thm

$f$ is  analytic in simple-connected $D$, for any $C_R(z_0)\in D$,

$$f(z_0)=\frac{1}{2\pi} \int_0^{2\pi} f(z_0+Re^{i\theta}) d\theta$$

전자기학에서 harmonic function의 또다른 특징을 배웠었는데, 경계가 아닌 내부의 점에서 nowhere extremum이라는 사실을 기억할 것이다. $\nabla u=0$이면서 모든 방향도함수가 0이 아니어야, 즉, $\nabla^2 u<0$또는 $\nabla^2 u>0$이어야 극점을 가지는데 해석적이라 0일 수 밖에 없다. analytic $f=u+iv$라 하면 $u$와 $v$는 harmonic이고 $|f(z)|^2=u^2+v^2$에 $\nabla^2$를 취해보면 마찬가지로 0이다. 따라서 다음의 정리도 증명된다.

 

THM 5-5 : Extreme value thm

$f$ is  analytic in simple-connected $D$ and is not a constant. Then $\nexists  z_0 \in D$ s.t. $|f(z_0)|$ is extreme.

 

따라서 최대값은 $\partial \bar{D}$에서만 존재하게 된다. 만약 복소평면 전체에서 해석적이고 유계(bounded)라면 최대값이 존재한다고 가정했을 때 THM 5-5를 위배하므로 상수함수일 수 밖에 없게 되는데, 이것을 Riouville's thm이라 한다. 또 눈여겨 볼 만한 것으로, $f(z)$가 $D$에서 유계일 때, 즉 $|f(z)|\leq M$이라면 Cauchy-integral formula와 간단한 inequality로부터 다음의 부등식을 얻는다.

$$|f^{(n)}(z_0)|=\left| \frac{n!}{i2\pi} \int_{C_R(z_0)} \frac{f(z)dz}{(z-z_0)^{n+1}}\right| \leq \frac{n!}{2\pi} \left| \int_{C_R(z_0)} \frac{|f(z)|}{|z-z_0|^{n+1}}\right| |dz| \leq \frac{n!}{2\pi} \frac{M}{R^{n+1}}2\pi R = \frac{n!M}{R^n}$$

이 부등식을 Cauchy-inequality라 한다. 사실 Liouville 정리와 Cauchy-ineqality는 그냥 그때그때 떠올려서 활용할 법 하므로 따로 THM으로 언급하지 않겠다. 다음의 대수학의 기본정리의 축소판을 증명해보자. 우리는 이 포스트 마지막에서 진짜 대수학의 기본정리를 증명할 것이다.

 

Q 5-1 : (축소판 대수학의 기본정리) If $P$ is a polynomial of order $n\geq 1$, $P$ has at least a zero.

 

A 5-1 : nowhere zero라고 가정해보자. $P\neq 0$ for all $z\in\mathbb{C}$. 따라서 $f(z)=1/P(z)$ 는 entire function이다.

$$|f(z)|=\frac{1}{|z|^n}\frac{1}{\left| a_n + \frac{a_{n-1}}{z} + \frac{a_{n-2}}{z^2} + \cdots + \frac{a_0}{z^n} \right|}$$

$|z| \to \infty$일 때 우변이 0에 수렴하므로 $\forall z \notin C_R(0)$, $|f(z)|<1$인 $R$이 존재한다. 그리고 유계 폐집합 $C_R(0)$에서도 실함수 $u$와 $v$가 유계이므로 $|f(z)|$도 유계이다. 따라서 모든 $z$에 대해서 $|f(z)|\leq K$라 할 수 있고 Liouville thm에 의하면 이것은 상수함수이고 가정에 모순된다. 따라서 적어도 하나의 영점을 가진다.

이제 Complex Analysis for physicists (2)에서 살펴보았던 급수의 개념을 조금 확장하고자 한다.

THM 5-6 : Taylor's Thm

$f$ is analytic in $G$, $D_R(a)\in G$. Then Taylor series of $f$ (RHS of the following)

$$f(z)=\sum_{k=0}^{\infty} \frac{f^{(k)}(a)}{k!}(z-a)^k$$

is convergent to $f(z)$ (LHS) for all $z\in D_R(a)$. Furthermore, $\forall r\in (0,R)$, uniformly convergent in $\bar{D}_r(a)$.

이것의 증명은 Cauchy integral formula를 포함하는데, 가슴으로 받아들여지지 않는다면 다른 곳에서 증명을 찾아보도록 하자.(나는 이것의 증명에 관심이 없다.) 우리가 어떤 함수를 멱급수로 나타냄에 있어서 강력한 tool을 소개하려고 한다. 바로 멱급수의 유일성(uniqueness)인데, 이것이 보장된다면 우리가 어떤 방법으로 멱급수를 얻든 그것이 유일하게 정답임을 알 수 있다. 즉, 알고있는 어떤 사실로부터 출발해서 얻든 멱급수가 유일하니까 그것이 답이라는 것이다.

THM 5-7 : uniqueness of power series

For $z \in D_r(a)$, suppose $f(z)=\sum_{n=0}^{\infty} a_n(z-a)^n = \sum_{n=0}^{\infty} b_n(z-a)^n$. Then $a_n=b_n$.

그런데 어떤 $f(z)$가 $D_R(a)$에서는 analytic하지 않지만, punctured disk $D^*_R(a)$에서는 analytic일 수도 있을 것이다. 그런 함수는 자명하게도 $z=a$에 대한 Taylor series가 존재하지 않을 것이나, 차수를 음의 영역까지 늘리게 되면 급수화할 수 있고, 이것을 Laurent series라 한다. 즉, $\sum_{-\infty}^{\infty}c_n (z-a)^n$이 수렴하면 by definition, Laurent series라 한다. 이 series가 annulus $A(a,r,R)=\{z\: : \: r<|z-r|<R\}$에서 수렴한다면 $r<s<t<R$인 $s$, $t$에 대하여 $\bar{A}(a,s,t)$에서 평등수렴이다. 이제 THM 2-18을 더 확장하여

THM 5-8 : Laurent Thm

$0\leq r<R$, $f$ is analytic in $A(a,r,R)$. For any $\rho \in (r,R)$, $\forall z_0 \in A(a,r,R)$, $f(z_0)$ can be represented by Laurent series of

$$f(z_0)=\sum_{n=-\infty}^{\infty} c_n(z_0-a)^n,\:\:\:\: c_n=\frac{1}{i2\pi}\int_{C_\rho^+(a)}\frac{f(z)}{(z-a)^{n+1}} $$

which is uniformly convergent in $\bar{A}(a,s,t)$.

멱급수의 유일성 정리 역시 다음과 같이 확장된다.

THM 5-7 (2) : uniqueness of Laurent series

For $z \in D_r(a)$, suppose $f(z)=\sum_{n=-\infty}^{\infty} a_n(z-a)^n = \sum_{n=-\infty}^{\infty} b_n(z-a)^n$. Then $a_n=b_n$.

이 정리들은 따지고보면 Cauchy-integral formula로부터 나온 결론이지만, 반대로 우리가 이것을 받아들이고 나면, Cauchy-integral formula도 자연스럽게 증명된다. 우선 적당한 영역에서 수렴하는 Laurent series를 생각하자.
$$f(z)=\sum_{n=-\infty}^{\infty} c_n (z-z_0)^n$$
적당히 $C_r(z_0)$의 궤적에서 적분을 수행하면 우변의 양의차수는 모두 Cauchy-Goursat thm에 의해 0이되고, $n=-2,-3,\cdot$에 대해서도 궤적의 매개변수화로 적분해보면 모두 0이되며, 오로지 $n=-1$에 대해서만 살아남고 다음의 식을 얻는다.
$$\frac{1}{i2\pi} \int_{C_r(z_0)} f(z)dz = c_{-1}$$
이번에는 $(z-z_0)^{-m}$을 양변에 곱하고 같은 궤적에서 적분을 수행하면 $m-1$차 항의 계수를 다음과 같이 얻는다.
$$\frac{1}{i2\pi} \int_{C_r(z_0)} \frac{f(z)}{(z-z_0)^m}dz = c_{m-1}$$
만약 $f(z)$가 analytic했다면, Taylor thm에 의해 진작 이것이 Cauchy-integral formula의 증명이 되며, punctured region에서 analytic했다면 위와 같이 Laurent series의 계수를 결정할 수 있다. 이것은 무언가 강한 인상을 남긴다. 마치 유한한 점에서 analytic하지 않은 영역에서의 적분마저도 series로 전개하여 적분값을 구할 수 있을 것만 같다. 그 적분 영역이 어떻게 생겨먹었든, Cauchy-goursat thm과 경로변경으로 인해 이미 적분경로에 대해서 자유로워 진 지는 한참 되었지 않은가? 이 아름다운 논의는 뒤로하고, 좀 더 수학적으로 엄밀한 논의를 위해 analytic하지 않은 점들과 0이되는 zero pt들을 분류해보자.

DEF 5-1 : singularity와 zero pt의 분류

$f$가 $z=a$에서 해석적이지 않으며, a의 근방에서는 analytic이라고 하자. (즉, isolated)

(1) $n=-1,\:-2,\:-3,\: \cdots$에 대하여 Laurent series의 계수 $c_n=0$이면, removable singularity를 갖는다. 

(2) Laurent series의 계수가 $c_{-k}\neq 0$이지만, $n<-k$에 대해서는 $c_n=0$이면 pole of order k라 한다.

(3) Laurent series가 무한히 많은 음의 정수 $n$에 대하여 $c_n\neq 0$이면 essential singularity라 한다.

$f$가 $D_R(a)$에서 analytic하고 $f^{(n<k)}(a)=0$이지만, $f^{(k)}(a)\neq 0$이라면, zero of order k라 한다. 이 때 $f$의 Taylor series 계수는 $c_{n<k}=0$이다.

몇 가지 예시를 들어보자. $f(z)=\frac{\sin z}{z}$는 $z=0$에서 analytic하지 않고 근방에서는 analytic이며 $f(0)=0$으로 우리가 정의해주기만 하면 모든 점에서 analytic이다. 우리는 $\sin z$의 급수를 알고있고, 이를 이용하여 Laurent series로 나타내면 $f(z)=\frac{1}{z} \left( z-\frac{z^3}{3!}+\cdots \right)$인데, 유일성 정리에 의해 이것이 바로 유일한 Laurent series가 된다. 비록 $z=0$에서 analytic하지 않아도 마치 급수에서는 $z=0$에서 analytic한 것처럼 보인다. 이런 경우 우리가 analytic하지 않은 점을 그저 함수값을 그 점으로의 극한으로 정의해주기만 하면 제거가 가능하다고 하여 removable이라 한다.

$f(z)=\sin \frac{1}{z}$는 당연히 $z=0$에서 analytic하지 않고 마찬가지로 $\sin z$의 급수를 알고있고, 그저 $z$대신에 $1/z$를 대입하면 그것이 유일한 Laurent series이고, $f(z)=\frac{1}{z}-\frac{1}{3!z^3}+\cdots$이다. 따라서 정의에따라 essential singularity이다. 그러나 이 같은 경우 극점들의 집합을 생각해 봤을 때 $z=0$은 극점 집합의 acc pt임을 알 수 있다. (essential singularity와 어떠한 상관이 있는가?)

zero pt와 pole pt의 차수에 대해서 조금 더 일반적인 논의를 해보자. 당연하게도 다음의 명제들을 간단하게 증명해보일 수 있을것이다.

THM 5-8 : 

(1) If $f$ has a pole of order k at $z=z_0$, then $\exists$ analytic $g(z)$ s.t. $f(z)=\frac{g(z)}{(z-z_0)^k}$, $g(z_0) \neq 0$.

(2) If $f$ has a zero of order k at $z=z_0$, then $\exists$ analytic $g(z)$ s.t. $f(z)=g(z)(z-z_0)^k$, $g(z_0) \neq 0$.

(3) If $f$ has a pole of order k at $z=z_0$, $\frac{1}{f(z)}$ has a zero of order k at the same pt.

(4) If $f$ and $g$ have a zero of order k at $z=z_0$, then $\frac{f}{g}$ has removable singularity at the same pt and can be defined $\frac{f(z_0)}{g(z_0)}=\lim_{z\to z_0} \frac{f}{g}$.

isolated singularity와 그 주변 점에서 복소함수의 거동에 대해서 몇 가지를 더 알아보자.

THM 5-9 :

(1) If $f$ is analytic and bounded in $D_r^*(a)$, then $f$ is analytic or has removable singularity at $z=a$.

(2) If $f$ is analyticin $D_r^*(a)$, $f$ to be analytic at $z=a$ is equivalent to $\exists ! \: \lim_{z\to a} f(z)$.

(3) If $f$ is analyticin $D_r^*(a)$, $f$ to have pole of order k at $z=a$ is equivalent to $\lim_{z\to a} |f(z)| =\infty$.

(4) If $f$ is analyticin $D_r^*(a)$, $f$ to have a essential singularity at $z=a$ is equivalent to $\nexists \: \lim_{z\to a} |f(z)|$.

위 정리들의 증명은 어렵지 않다. 우선 (1)부터 증명해보자. 다음의 함수를 생각하자.
$$g(z)=(z-a)^2 f(z)\:\: (z\neq a)\:\:\:\: g(a)=0$$
자명하게도 $g$는 $D^*_r(a)$에서 analytic인데, $g'(a)=\lim_{z\to a} \frac{g(z)-g(a)}{z-a}=\lim_{z\to a} (z-a)f(z)=0$이고($f$가 유계이므로), $g$또한 $a$에서 해석저기고 $g(a)=g'(a)=0$이다. Taylor thm에 의해 $\forall z\in D_r(a)$에 대하여 Taylor series를 가지는데, 이 Taylor series에 $(z-a)^2$을 나누면 다음을 얻는다.
$$f(z)=\sum_{n=2}^{\infty}\frac{g^{(n)}(a)}{n!}(z-a)^n=\sum_{n=0}^{\infty}\frac{g^{(n+2)}(a)}{(n+2)!}(z-a)^n$$
$f(a)=\frac{g^{(2)}(a)}{2!}$로 정의하면 $f$는 $a$에서 analytic이다.

(2)는 (1)로부터 간단하게 증명되고, (3)을 증명해보자. $f$가 $a$에서 pole of order k라면 THM 5-8에 의해 $f(z)=\frac{h(z)}{(z-a)^k}$이고, $h$는 $a$에서 analytic이고 $h(a) \neq 0$이다. $\lim_{z\to a} |h(z)|=|h(a)|\neq 0$이고 $\lim_{z\to a} |(z-a)|=0$이므로 $\lim_{z \to a}|f(z)|=\infty$이다. 역으로, $\lim_{z \to a}|f(z)|=\infty$를 가정하면 극한의 정의에 의해 $z\in D_\delta^*(a)$이면 $|f(z)|>1$를 만족하는 어떤 $\delta>0$이 존재해야 하고, 따라서 $1/f(z)=g(z)$는 $D_\delta^*(a)$에서 analytic & bounded이다. ($|g(z)|\geq 1$) (1)에 의해 $a$에서 $g$를 정의할 수 있고 그 $g$는 $D_\delta^*(a)$ 전체에서 analytic이다. $|g(a)|=\lim_{z\to a}\frac{1}{|f(z)|}=0$이므로 $a$는 $g$의 zero pt가 된다. 즉 $a$에 대해서 유한차수가 되어야 하고(그렇지 않으면 모든 도함수가 0이고, Taylor thm에 의해 원함수도 0이다.) $g(z)=\frac{1}{f(z)}$는 $D_\delta^*(a)$에서 analytic이므로 이 결과는 불가능하고, $a$에서 $g$가 zero of order k라 할 수 있다.

마지막으로 모든 singularity가 removable or pole of order k or essential이고, 앞의 두 경우를 제외하면 가능한 $\lim_{z\to a} |f(z)|$는 없다. 즉 이 극한값이 존재하지 않는 것과 essential singularity를 가지는 것은 동치이다.

이제 본격적으로 복소적분에 대한 영감을 수학적으로 기술할 준비가 되었다. 적분경로 내에 유일한 pole $z=a$을 가지고 위에서 Laurent series의 계수를 결정하는데 있어서 다음의 등식을 얻었다. (경로변경과 Cauchy-goursat thm에 의해 적분경로를 바꿔 적으면)
$$\int_{C} f(z)dz = i2\pi c_{-1},\:\:\:\:(z_0 \in C)$$
만약 pole을 여러개 가져도 경로를 나누면 되므로 그저 합해주면 될 뿐이다. 이것이 명시해주는 것은 $f(z)$의 어떤 경로 $C$내에서의 적분은, 그 내부에서의 Laurent series의 $c_{-1}$만 알아내면 값을 아주 쉽게 구한다는 것이다. 그렇다면 우리는 이제 $c_{-1}$을 계산하는 방법만 알면 되겠다. 이 $c_{-1}$을 유수(Residue)라 하고, $c_{-1}=Res[f,a]$와 같이 표기한다.

THM 5-10 : Residue Thm

$C$ is simple-closed path in simple-connected $D$. If $f$ is analytic in $\partial C \cup C - {z_1, z_2, z_3, \cdots, z_n}$,

$$\int_C f(z) dz = i2\pi \sum_i Res[f,z_i]$$

말로는 Laurent series의 $c_{-1}$을 구하면 된다지만 실제로 함수가 주어졌을 때 일일이 급수화 하고 있을 수는 없다. $f$가 $a$에서 pole of order k라면
$$f(z)=\frac{c_{-k}}{(z-a)^k}+\frac{c_{-k+1}}{(z-a)^{k-1}}+\cdots+\frac{c_{-1}}{z-a}+\cdots$$
양변에 $(z-a)^k$를 곱하고 k-1번 미분한 후 극한 $z\to a$를 취해주면
$$c_{-1}=Res[f,a]=\frac{1}{(k-1)!}\lim_{z\to a} \frac{d^{k-1}}{dx^{k-1}}\left[ (z-a)^k f(z) \right]$$
이제 남은 문제는 이 극한을 효율적으로 잘 계산하고, 모든 유수에 대해서 잘 더하는 것 뿐이다. 나름의 테크닉이라면, L'hospital Rule을 적절히 활용하는 것과 부분분수로 잘 나타내 보는 것 정도이다.

Q 5-2 : Evaluate $Res \left[ \frac{\pi cot(\pi z)}{z^2}, 0 \right]$

A 5-2 :
$\sin(\pi z)$가 0에서 zero of order 1이므로, $f$ 전체의 pole order는 3이다.(THM 5-8) L'hospital Rule에 의하면 
$$Res[f,0]=\frac{1}{2}\lim_{z\to 0} D^2 \pi z cot(\pi z)=\frac{1}{2} \lim_{z\to 0} \frac{\pi z \cos(\pi z)-\sin(\pi z)}{\sin^2(\pi z)}\\ =\pi^2 \lim_{z\to 0} \frac{-\pi^2 z \sin(\pi z)+\pi cos(\pi z) - \pi \cos(\pi z)}{3\pi \sin^2(\pi z)\cos(\pi z)}=\lim_{z\to 0} \frac{-\pi^3 z}{3\sin(\pi z) \cos(\pi z)} = -\frac{\pi^2}{3}$$

다른 다양한 예시문제로는 아래의 링크 Q1 정도를 참고하자.
physvillain.tistory.com/3

[ PART II ]

이제는 삼각함수가 포함된 적분을 살펴보자. 보통 $\int_0^{2\pi} F(\cos \theta, \sin \theta) d\theta$와 같은 꼴의 적분은 $z=e^{i\theta}$로 치환하여 $C_1(0)$에 대한 복소적분으로 치환해 생각해볼 수 있다. 이 때 $\sin \theta = \frac{z-z^{-1}}{2i}$, $\cos \theta = \frac{z+z^{-1}}{2}$로 두면 자연스럽게 적분경로 내부에 pole이 있는 유수적분이 될 것이다. 다음의 예시를 보자.

Q 5-1 : Evaluate $\int_0^{2\pi} \frac{d\theta}{1+3\cos^2 \theta}$. (문제 출처 : J. H. Mathews & R. W. Howell, Complex Analysis for mathematics and engineering)

A 5-1 (1) : 먼저 피적분함수 $\frac{1}{1+3\cos^2 \theta}$의 부정적분을 적당히 찾아보자. $1=\sin^2 \theta + \cos^2 \theta$임을 이용하고, $\cot \theta$의 미분이 $-\csc^2 \theta$임을 이용하여
$$\frac{1}{1+3\cos^2 \theta}=\frac{1}{\sin^2 \theta + 4 \cos^2 \theta} = \frac{\csc^2 \theta}{1+(2\cot \theta)^2}=-\frac{1}{2} \frac{-2\csc^2 \theta}{1+(2\cot \theta)^2} \\ \int \frac{d\theta}{1+3\cos^2 \theta} = -\frac{1}{2} \arctan(2\cot \theta) +C$$
그런데 적분영역 $[0,2\pi]$에서 과연 $\frac{1}{1+3\cos^2 \theta}$의 부정적분이 $-\frac{1}{2} \arctan(2\cot \theta)$일까? 첫 번째 문제는 $\cot \theta$가 $\theta=0, \pi, 2\pi$에서 함수값이 부정(undefined)인 문제가 있다. 이 문제는 $g(\theta)=-\frac{1}{2} \arctan(2\cot \theta)$라 했을 때, $\theta=0$과 $\theta=2\pi$일 때는 $g(0)=\lim_{\theta \to 0+} g(\theta)=-\frac{\pi}{4}$로 정의하면 되고, $g(2\pi)=\lim_{\theta \to 2\pi-} g(\theta)=\frac{\pi}{4}$로 정의하면 된다. 그런데 $\theta=\pi$일 때는 어떠한가? 좌극한과 우극한이 다른 것을 알 수 있을 것이다. $\lim_{\theta \to \pi-} g(\theta) = \frac{\pi}{4}$이고, $\lim_{\theta \to \pi+} g(\theta) = -\frac{\pi}{4}$이다. $[0,\pi)$와 $(\pi,2\pi]$에서는 이것이 부정적분이 되지만 $[0,2\pi]$에서는 부정적분이 아니라는 것이다. 

 

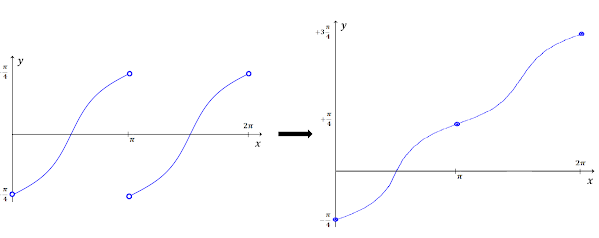
한 부정적분을 연속으로 만드는 방법 중 하나는 그저 "이어 붙이는 것"이다. (왼쪽의 상황에서 미적분학의 기본정리가 성립하는가?) 강제로 연속으로 만들되, 미분은 보존할 방법이 이어 붙이는 것이다. 부정(undefined)점에서 함수값을 극한값으로 정의해주고, $\theta=\pi$에서 좌우극한을 이어붙인 함수는 위와 같을 것이다. 따라서 정적분값은 미적분학의 기본정리에 의해 $\pi$가 된다.

A 5-1 (2) : 이번에는 $z=e^{i\theta}$의 치환을 이용하여 경로적분을 수행한다.
$$\int_0^{2\pi} \frac{d\theta}{1+3\cos^2 \theta} = \frac{4}{i} \int_{C_1(0)} \frac{z dz}{(3z^2+1)(z^2+3)}=8\pi \sum_i Res \left[ \frac{z}{3z^4+10z^2+3}, z_i=\pm \frac{1}{\sqrt{3}} \right] \\=8\pi \sum_i \lim_{z \to z_i}\frac{(z-z_i)z}{(3z^2+1)(z^2+3)}=2\pi \sum_i \frac{1}{3z_i^2+5}=\pi$$

실적분을 복소적분으로 바꾸어서 쉽게 풀리게 되는 대표적인 예시는 유리(rational)함수의 이상(improper)적분이다. 일반적으로 적분 $\int_{-\infty}^{\infty} f(x) dx$를 해석하는 방법은 다양하겠지만, 아래의 대표적인 두 가지를 보자.
$$\int_{-\infty}^{\infty} f(x) dx = \left( \lim_{a \to -\infty} \int_{a}^0 + \lim_{b \to \infty} \int_0^b \right) f(x) dx \:\:\: \cdots \:(1) \\ \int_{-\infty}^{\infty} f(x) dx = \lim_{R \to \infty} \int_{-R}^R f(x) dx \:\:\: \cdots \: (2)$$
(1)의 극한은 존재하지 않지만, (2)의 극한은 존재할 수 있는데 이 극한 (2)가 존재한다면 이 값을 코시주치(Cauchy principal value)라 한다. 이 포스트에서 논하는 이상적분들은 별다른 표기 없이 Cauchy 주치를 의미한다.

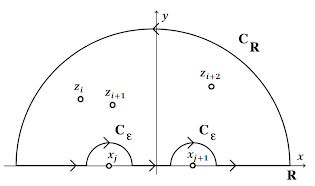
만약 차수가 $m$, $n$인 다항함수 $P(x)$와 $Q(x)$에 대해 유리함수 이상적분 $\int_{-\infty}^{\infty} \frac{P(x)}{Q(x)}dx$를 복소적분으로 바꾸어 풀 조건은 $n\geq m+2$이고, 적분영역은 다음과 같다. 아래 그림과 같은 적분경로를 C라 하자.

우선 경로 반시계방향 상반원 경로 $C_R$에 대하여 적분값을 0으로 만들고 싶다. R이 충분히 크면 (대략)
$$\int_{C_R} \frac{P(z)}{Q(z)} dz \simeq \int_{C_R} R^{n-m} dz \leq \int_{C_R} |R^{n-m}| |dz| =\int_0^{2\pi} R^{n-m} R d\theta \sim R^{n-m+1}$$
$R\to\infty$일 때 이 값이 사라지려면 $n\geq m+2$이어야 한다. 또, simple pole이 x축 위에 $x=x_j$에 있는 경우 $0\leq \theta \leq \pi$에 대하여 경로 $-C_\epsilon$이 $-C_\epsilon : z=x_j+re^{i\theta}$라면 다음이 성립한다.
$$\lim_{r\to 0} \int_{-C_\epsilon} f(z) dz = i\pi Res [f,x_j]$$
간단하게 이것을 증명해보면, $z=x_j$에서 Laurent series는 $f(z)=\frac{Res[f,x_j]}{z-x_j}+g(z)$꼴인데, 여기서 $g(z)$는 $z=x_j$에서 analytic이다. $-C_\epsilon$의 매개변수 식으로부터
$$\int_{-C_\epsilon} f(z)dz = Res[f,x_j] \int_0^{\pi} \frac{ire^{i\theta} d\theta}{re^{i\theta}} + ir\int_0^{\pi}g(x_j+re^{i\theta})e^{i\theta}d\theta \\ = i\pi Res[f, x_j]+ir\int_0^{\pi}g(x_j+re^{i\theta})e^{i\theta}d\theta$$
을 얻는데, $g$가 $x_j$에서 연속이므로, $|g(x_j+re^{i\theta})| \leq M$을 만족하는 $M$이 존재.
$$\left| \lim_{r \to 0} ir \int_0^{\pi} g(x_j+re^{i\theta})e^{i\theta} d\theta \right| \leq \lim_{r \to 0} r \int_0^{\pi} M d\theta = 0$$
이로써 $\lim_{r\to 0} \int_{-C_\epsilon} f(z) dz = i\pi Res [f,x_j]$임을 증명하였고, 적분영역을 실축 전체와 상반원 $C_R$로 잡으면 실축의 simple pole을 회피하여 지나간 경로에 $-C_\epsilon$들의 경로를 더해준 것과 같다.
$$\int_{C_R}+\int_{-\infty}^{\infty}=\int_C + \sum \int_{-C_\epsilon}$$
$C_R$에 대한 적분이 0으로 가도록 잡았으므로, 실적분의 결과는 다음과 같이 된다.
$$\int_{-\infty}^{\infty} \frac{P(x)}{Q(x)} dx = i2\pi \sum_i Res \left[ \frac{P}{Q}, z_i \right] + i\pi \sum_j Res \left[ \frac{P}{Q}, x_j \right]$$

한가지 더 살펴볼만한 주제가 있다. integrand에 유리함수에 삼각함수가 곱해진 꼴인 경우이다.
$$\int_{-\infty}^{\infty} \frac{P(x)}{Q(x)} \sin(kx) \: or \: \cos (kx) dx$$
당연하게도 삼각함수는 $e^{ikz}$의 실/허수부로 표현되므로 다음과 같은 적분을 상반원+실축 경로에서 수행한다고 가정하자. 우리는 상반원 경로 $C_R$에 대한 적분이 0으로 만들고 싶다. 다음의 정리를 보자.

THM 5-1 : Jordan Lemma

$P$ and $Q$ are m, n th order polynomials ($n\geq m+1$). Then

$$\lim_{R \to \infty} \int_{C_R} \frac{e^{iz}P(z)dz}{Q(z)}=0$$

조금 식을 전개해보면 자명한 것으로 보인다. $|z|\to\infty$일 때 $|P/Q|\to 0$이므로 극한의 정의에 따라

$\forall \epsilon>0$, $\exists R_\epsilon$ such that if $|z| \geq R_\epsilon$, $\left| \frac{P(z)}{Q(z)} \right| < \frac{\epsilon}{\pi}$.

$|dz|=Rd\theta$, $|e^{iz}|=e^{-R\sin{\theta}}$이고, $0\leq \theta \leq \frac{\pi}{2}$에서 $0\leq \frac{2\theta}{\pi} \leq \sin{\theta}$이므로
$$ \left| \int_{C_R} \frac{e^{iz}P(z)dz}{Q(z)} \right| \leq \int_{C_R} \frac{\epsilon}{\pi} |e^{iz}| |dz| = \frac{\epsilon}{\pi} \int_0^{\pi}e^{-R\sin{\theta}}R d\theta \\ =\frac{2\epsilon}{\pi} \int_0^{\frac{\pi}{2}} e^{-R\sin\theta}Rd\theta \leq \frac{2\epsilon}{\pi} \int_0^{\frac{\pi}{2}} e^{\frac{-2R\theta}{\pi}}R d\theta = \epsilon(1-e^{-R}) < \epsilon$$

이제 $C_R$에서 적분값이 0임을 보였으므로, 본격적으로 적분을 수행해보자.
$$\left( \int_C+\sum \int_{-C_\epsilon} \right) \frac{P(z)}{Q(z)}e^{-ikz} =\left( \int_C+\sum \int_{-C_\epsilon} \right) \frac{P(z)}{Q(z)} \left[ \cos(kz)+i\sin(kz) \right] dz \\= i2\pi \sum_{i} Res \left[ \frac{P}{Q}e^{-ikz}, z_i \right] + i\pi \sum_j Res \left[ \frac{P}{Q}e^{-ikz}, x_j \right]$$
각각의 실수부와 허수부를 같게 두면 다음과 같은 결론을 얻는다.

THM 5-2 :
$P$ and $Q$ are m, n th order polynomials ($n\geq m+1$), then

$$\int_{-\infty}^{\infty} \frac{P}{Q} \cos(kx) dx = -2\pi \sum_i \Im \left( Res \left[ \frac{P}{Q}e^{-ikz}, z_i \right] \right) - \pi \sum_j \Im \left( Res \left[ \frac{P}{Q}e^{-ikz}, x_j \right] \right) \\ \int_{-\infty}^{\infty} \frac{P}{Q} \sin(kx) dx = 2\pi \sum_i \Re \left( Res \left[ \frac{P}{Q}e^{-ikz}, z_i \right] \right) + \pi \sum_j \Re \left( Res \left[ \frac{P}{Q}e^{-ikz}, x_j \right] \right)$$

 

사실 이것을 공식화한 이유는 아래 링크 ('18 Advanced Calculus 기말 기출)의 1-(d) 문제를 풀면서 떠올랐기 때문인데, 이 것을 공식화해두면 나중에 양자역학이나, 양자장론에서 매우 편하다. 

physvillain.tistory.com/3 

 

보통 공학수학(고등미적) 과정에서는 이것을 따로 공식화하지 않으므로 위 링크의 풀이 같은 논증이 필요할 것이다. (나도 처음에는 상반원 $C_R$에서의 0으로의 수렴성을 보이는 것이 어려웠다.) 이것을 이용한 다른 문제를 살펴보자. 너무 뻔하거나 난이도가 낮지는 않은 것으로 골라봤다.

Q 5-2 : Evaluate Cauchy PV of $\int_{-\infty}^{\infty} \frac{\sin^2 x}{x^2}dx$.

A 5-2 : $\sin^2 x$를 $\cos (2x)$로 표현하고, odd function을 더해도 같음을 이용한다.
$$\int_{-\infty}^{\infty} \frac{\sin^2 x}{x^2}dx = \int_{-\infty}^{\infty} \frac{1-\cos(2x)}{2x^2}dx = \int_{-\infty}^{\infty} \frac{1-\cos x}{x^2} dx =\int_{-\infty}^{\infty} \frac{1-\cos z -i\sin z}{z^2}dz \\ = \int_{-\infty}^{\infty} \frac{1-e^{iz}}{z^2} dz = \left( \int_C+\sum \int_{-C_\epsilon} \right) \frac{1-e^{iz}}{z^2} dz = i\pi \lim_{z \to 0} \frac{1-e^{iz}}{z} =\pi$$

Q 5-3 : (Fresnel integral) Evaluate $\int_0^{\infty} \sin^2 x dx$, $\int_0^{\infty} \cos^2 x dx$.

A 5-3 : 적분경로를 다음과 같이 잡자. ($R\to\infty$)
$K_1 : \theta=0,\: 0\leq r \leq R$,   $K_2 : r=R, \:0\leq \theta \leq \pi/4$,   $K_3 : \theta=\pi/4, \: R\geq r \geq 0$
Cauchy-Goursat Thm에 의해 아래의 적분값은 0이다.
$$\left( \int_{K_1} + \int_{K_2} + \int_{K_3} \right) e^{-z^2} dz = \int_0^{\infty} e^{-x^2} dx + 0 + \int_{\infty}^0 e^{-ir^2}\frac{1+i}{\sqrt{2}} dr \\ = \frac{\sqrt{\pi}}{2} - \frac{1}{\sqrt{2}} \int_0^{\infty} (\cos(r^2)-i\sin(r^2))(1+i) dr = 0$$
실수부와 허수부에 대한 등식을 세우면
$$\int_0^{\infty} \cos(r^2)-\sin(r^2) dr = 0, \:\:\:\: \int_0^{\infty} \sin(r^2)+\cos(r^2) dr = \sqrt{\frac{\pi}{2}} \\ \therefore \int_0^{\infty} \sin(x^2) dx = \int_0^{\infty} \cos(x^2) dx = \sqrt{\frac{\pi}{8}}$$

이것을 Fresnel integral이라 하며, 0부터 $x$까지의 정적분을 $S(x)$, $C(x)$라 한다. 이름에서부터 느껴지겠지만 이것은 광학에서 사용된다. Fresnel integral을 조금 더 일반화 하여 얻어보자.

Q 5-4 : 다음의 적분을 계산하여라. (허수부는 sine, 실수부는 cosine에 대한 적분을 얻는다.)
$$\int_0^{\infty} x^m \exp(ix^n)dx $$

A 5-4 : 이것을 먼저 바로 풀기보다 이런 형태의 부정적분을 series expansion으로 혹은 우리가 알고있는 special function들의 basis로 전개할 수 있을 것이다. 가장 간단한 경우부터 살펴보자.
$$\int x\cos(a_0+a_1x) dx = \frac{1}{a_1^2} \cos(a_0+a_1 x)+ \frac{x}{a_1} \sin(a_0+a_1 x) \\ \int x\sin(a_0+a_1x) dx = \frac{1}{a_1^2} \sin(a_0+a_1 x)- \frac{x}{a_1} \cos(a_0+a_1 x)$$
또, integral py parts를 반복하고 실/허수부를 나누어 다음의 식을 얻는다.
$$\int x^n e^{iax} dx = \frac{e^{iax}}{ia^{n+1}} \sum_{k=0}^{n} \frac{n! i^k(ax)^{n-k}}{(n-k)!} \\ \int x^n \cos(ax) dx = \sum_{k=0}^n \frac{n!}{(n-k)!}\frac{x^{n-k}}{a^{k+1}} \sin (ax+k\pi/2) \\ \int x^n \sin(ax) dx = -\sum_{k=0}^n \frac{n!}{(n-k)!}\frac{x^{n-k}}{a^{k+1}} \cos (ax+k\pi/2)$$
sine/cosine의 합공식은 다음 identity의 실/허수부이다.
$$\exp\left( i\sum_{j=0}^l a_j x^j \right) = \exp(ia_0) \exp\left( i\sum_{j=1}^l a_j x^j \right)$$
또 $y=x^2$의 치환에 의해 다음의 식이 성립한다.
$$\int_0^u x^{2m+1} \exp(ix^{2n})dx = \frac{1}{2} \int_0^{u^2} y^m \exp(iy^n)dy$$
이제 n차 Fresnel integral $\int \sin(x^n) dx$와 $\int \cos(x^n) dx$에 대해 살펴볼 준비가 끝났다. $x=y^{1/n}$의 치환과 integral by parts의 반복을 통해
$$\int e^{ix^n}=\frac{1}{n} \int y^{1/n-1}e^{iy}dy = \frac{1}{in} y^{1/n-1} e^{iy} - \frac{1}{in} ( \frac{1}{n} - 1 ) \int y^{1/n-2}e^{iy}dy \\ = \frac{1}{in} y^{1/n-1}e^{iy}-\frac{1}{in}(\frac{1}{n}-1)-\frac{1}{i^2n}(\frac{1}{n}-1)y^{1/n-2}e^{iy} \\ +\frac{1}{i^2n}(\frac{1}{n}-1)(\frac{1}{n}-2)\int y^{1/n-3}e^{iy}dy=\cdots$$
Taylor expansion으로부터 $\int \sin(x^n) dx$는
$$\int \sin(x^n) dx = \int \sum_{l=0}^{\infty}\frac{(-1)^l x^{n(2l+1)}}{(2l+1)!}dx=\sum_{l=0}^{\infty}\frac{(-1)^l x^{2nl+n+1}}{(2nl+n+1)(2l+1)!}$$
cosine도 마찬가지로 전개할 수 있다.(생략) power series $f=\sum_{x\geq 0} b_s z^s$의 계수 $b_s$과 Neumann expansion $z^{\nu}f(z)=\sum_{s \geq 0} a_s J_{\nu+s}(z)$의 계수 $a_s$사이의 관계는 다음과 같다. (간혹 3D 퍼텐셜에 대한 양자역학 문제나 scattering에서 보았을 수도 있을 것이다.)
$$a_s=(\nu+s) \sum_{m=0}^{\lfloor s/2 \rfloor} 2^{\nu+s-2m} \frac{\Gamma(\nu+s-m)}{m!} b_{s-2m}$$
$\nu=1+1/n$, $z=x^n$을 대입하면 Fresnel integral의 Neumann basis로의 전개가 완성된다. 특별하게 n=2인 경우에 다음과 같이 전개된다.
$$\int \sin(x^2)dx = \frac{\sqrt{2\pi}}{2} \sum_{s\geq 0} J_{2s+3/2}(x^2)$$
$\int \sin(x^n) dx$의 power series에서 confluent hypergeometric function의 계수를 보았을 것인데 조금 더 일반화하여 다음의 적분을 보자.
$$\int x^m \sin(x^n) dx = \int \sum_{l=0}^{\infty} \frac{(-1)^l x^{m+2nl+m}}{(2l+1)!} dx = \sum_{l=0}^{\infty} \frac{(-1)^l x^{m+2nl+n+1}}{(m+2nl+n+1)(2l+1)!} \\ = \frac{x^{m+n+1}}{m+n+1} {}_1 F_2 \left( \frac{1}{2}+\frac{m+1}{2n} ; \: \frac{3}{2}+ \frac{m+1}{2n} , \: \frac{3}{2} ; -\frac{x^{2n}}{4} \right)$$
이것은 아래 exponential의 허수부에 해당한다.
$$\int x^m \exp(ix^n)dx = \int \sum_{l=0}^{\infty} \frac{i^l x^{m+nl}}{l!} dx = \sum_{l=0}^{\infty} \frac{i^l x^{m+nl+1}}{l! (m+nl+1)} \\ = \frac{x^{m+1}}{m+1} {}_1 F_1 \left( \frac{m+1}{n}; \: 1+\frac{m+1}{n} ; \: ix^n \right)$$
hypergeometric function의 Laurent series로부터 leading term은
$${}_1 F_1 \left( \frac{m+1}{n}; \: 1+\frac{m+1}{n} ; \: ix^n \right) \sim \frac{m+1}{n} \Gamma \left( \frac{m+1}{n} \right) e^{i\pi (m+1)/(2n)}x^{-(m+1)}$$
바로 위 식에 대입하고 극한을 취하여 다음 두 식을 얻는다.(아래는 $xc^{1/n}\to x$)
$$\int_0^{\infty} x^m \exp(ix^n)dx = \frac{1}{n} \Gamma \left( \frac{m+1}{n} \right) e^{i\pi(m+1)/(2n)} \\ \int_0^{\infty} x^m \exp(icx^n)dx = \frac{1}{nc^{(1+m)/n}} \Gamma \left( \frac{m+1}{n} \right) e^{i\pi(m+1)/(2n)}=\frac{i^{(1+m)/n}}{nc^{(1+m)/n}} \Gamma \left( \frac{m+1}{n} \right)$$
이것으로 (좀 많이) 일반화된 Fresnel 적분 결과를 유도해 내었다. (R. J. Mathar, "Series Expansion of Generalized Fresnel Integral", 2012)

다음으로 피적분함수가 branch cut을 갖는 경우를 살펴보자. 예를들어 $z^a=e^{a \ln z}=e^{a\ln|r| + ia \arg z}$와 같은 함수가 포함되어 있는 경우, 우리는 적분영역이 branch를 적절히 적분영역을 피해서 잘 선택해야 할 것이다. (위의 Q 5-1처럼 부정적분이 하나의 branch 한정해서만 부정적분이 된다. 실적분에서 보았듯이 이 적분같은 경우도 미적분학의 기본정리도 이 branch범위 내에서만 성립한다.) 다음의 예시를 보자.

(L) : Q 5-5의 적분영역, (R) : Q 5-6의 적분영역 (그림 수정 : 반시계방향)

Q 5-5 : Evaluate $\int_0^{\infty} \frac{\ln x dx}{x^2+a^2}$.

A 5-5 : 이것은 실적분인데, $z=0$에서 제거불가능한 singularity를 가진다.(: essential singularity) 그러므로 적분영역을 큰 반원과 원점 근처의 작은 반원을 포함하게 잡아야 한다. 중요한 것은 $\ln(x)$의 branch cut을 $\pi$가 아니라, 적당히 적분영역을 피해서 잡는 것이다. (그래야 미적분학의 기본 정리가 성립할 것이므로) 여기서는 $\arg z$의 branch cut을 $-\pi/2$로 잡는다. (위의 그림 왼쪽(L))
바깥 큰 상반원에 대한 적분은
$$\left| \int_{C_R} f(z) dz \right| \leq \int_{C_R} |f(z)| |dz| \leq \frac{R (\ln R+\pi) \pi}{R^2-a^2} \to 0$$
안쪽 작은 상반원에 대한 적분도
$$\left| \int_{-C_\epsilon} f(z) dz \right| \leq \int_{-C_\epsilon} |f(z)| |dz| \leq \frac{\pi R \ln R }{R^2+a^2} \to 0$$
남는것은 이제 실축위의 적분이다.
$$\int_C f(z) dz = \int_0^{\infty} \frac{\ln x dx}{x^2+a^2} + \int_{-\infty}^{0} \frac{\ln(-x)+i\pi }{x^2+a^2}dx \\ = 2 \int_0^{\infty} \frac{\ln x dx}{x^2+a^2} + i\pi \int_0^{\infty} \frac{dx}{x^2+a^2} = 2 \int_0^{\infty} \frac{\ln x dx}{x^2+a^2} + i\frac{\pi^2}{2a}$$
그런데 Residue Thm에 의해
$$\int_C f(z) dz = i2\pi\,Res[f,ai]=\frac{\pi \ln a}{a}+i\frac{\pi^2}{2a}$$
이므로 다음의 결과를 얻는다.
$$\int_0^{\infty} \frac{\ln x dx}{x^2+a^2}=\frac{\pi \ln a}{2a}$$

다른 대표적인 케이스로, 유리함수 모양에 $x^a$가 곱해진 경우($0<a<1$)의 예시를 보자.

Q 5-6 : $P$와 $Q$는 차수가 $m$, $n$인 다항함수($n \geq m+2$)이고, 양의실수에서 $Q(x) \neq 0$이고 원점에서 기껏해야 pole of order 1을 가진다. $f(z)=z^a P(z)/Q(z)$일 때($0<a<1$) 다음의 improper integral를 계산하여라. $P/Q$는 $z_1$, $z_2$, $z_3$, $\cdots$의 pole을 가진다.
$$\int_0^{\infty} f(x) dx$$

A 5-6 : 위 그림 오른쪽(R)과 같은 적분 경로를 생각하자. 우선 바깥의 큰 원 $C_R$과 안쪽의 작은 원 $C_r$에 대해서는 지금까지 했던 방법으로 극한이 0임을 보일 수 있다. $\arg z$의 branch cut을 0으로 잡으면 적분영역 내에서 미적분학의 기본정리가 성립하고, 실축 바로 위와 실축 바로 아래의 적분만이 남는다. $Q(x)$가 기껏해야 원점에서 simple pole이어야 하는 이유는, 실축위에서의 improper intergal이 수렴하지 않기 때문이다. (간단히 예시를 들어서 계산해보라.)
$$\int_C f(z) dz = \int_0^{\infty} \frac{e^{a\ln x} P(x)}{Q(x)} dx + \int_{-\infty}^{0} \frac{e^{a \ln (-x) + i 2a\pi} P(x)}{Q(x)} dx=i2\pi \sum_i Res[f,z_i]$$
따라서 다음의 결과를 얻는다.
$$\int_0^{\infty} \frac{x^a P(x)}{Q(x)}dx = \frac{i2\pi \sum_i Res[f,z_i]}{1-e^{i2a\pi}}$$

branch cut을 임의로 바꾸어 푸는 예시를 하나 더 살펴보자. 위에서 일반화한 Fresnel 적분의 결과를 사용하지 않고 아래의 적분을 계산해보자.

Q 5-7 : Evaluate $\int_0^{\infty} \frac{\sin x}{x} dx$.

A 5-7 (1) : 위 Q 5-5의 적분경로와 같은 경로를 잡고 $\int_C \frac{e^{iz}}{z} dz$를 계산하자.
무한 상반원 $C_R$에서는 간단하게 0으로 수렴함을 보일 수 있고, 원점에서는 Jordan Lemma에 의해 $-i\pi \,Res[f,0]$으로 수렴한다. 적분영역 내부에 pole이 없으므로 Cauchy-Goursat Thm에 의해 전체 적분값은 0이므로
$$\int_C \frac{e^{iz}}{z} dz = 2i\int_0^{\infty} \frac{\sin x}{x} dx -i\pi = 0$$
에서 아주 쉽게 $\pi/2$로 결정할 수 있다.

A 5-7 (2) : 사실 이것을 적당히 테크닉을 잘 사용하면 복소적분 없이도 풀 수 있다. Gauss integral $\int e^{-ax^2} dx$와 같은 꼴에서 a를 미분하여 얻는다던가, 혹은 전자기학에서 적분히 어려운 경우 적당한 변수 하나를 추가해 준 후 원시함수를 구하는 등의 trick을 본 적 있을 것이다. 여기에서도 다음과 같은 trick을 사용하자. ($y>0$)
$$\int_0^{\infty} \frac{\sin x}{x} e^{-yx} dx=-\frac{\partial}{\partial y}\int_0^{\infty} \frac{\sin x}{x} e^{-yx} dx = \left[ \frac{e^{-yx}}{y^2+1}(y\sin x + \cos x) \right]_{x=0}^{x=\infty} = -\frac{1}{y^2+1} \\ \int_0^{\infty} \frac{\sin x}{x} e^{-yx} dx = -\arctan y +C$$
그런데 $y\to \infty$이면 $0=-\pi/2 + C$이므로, $C=\pi/2$로 결정할 수 있고, $y=0$을 대입하여 $\int_0^{\infty} \frac{\sin x}{x} dx=\frac{\pi}{2}$를 얻는다.

여기서 눈치가 빠른 사람은 부정적분의 $\arg$부분이 하나의 branch에 국한된게 아니라, 그 다음 branch까지 이어진다면 어떻게 될 것인가? 예를들어 $f(z)$ 부정적분이 $|g(z)|+k \arg z^2$꼴인데, 적분영역이 $C_1(0)$이라면, 한 branch에서 단위원을 한바퀴 돌아가면(편의상 branch를 $0<\arg z \leq 2\pi$라 하자.) 그 부정적분을 복소평면에 궤적으로 나타낼 때 각도부분이 두 바퀴 돈다. ($0<\arg z \leq 4\pi$) $|g(z)|$야 닫힌 경로에서 어차피 적분값에 영향을 주지 못할 것이고, 두바퀴 돌아서 $4\pi k$의 적분값이 얻어져야 할 것이다. 이것이 왜 그러냐 하면, $0<\arg z \leq \pi$에서는 그 부정적분이  $|g(z)|+k Arg_{(branch=0)} z^2$이고, $\pi<\arg z \leq 2\pi$에서는 그 부정적분이 $|g(z)|+k (Arg_{(branch=0)} z^2+2\pi)$이기 때문이다. Q 5-1에서 실함수에 대한 부정적분을 미적분학의 기본 정리가 성립하도록 이어 붙인 것처럼 복소평면에서 복소평면으로 대응할 경우에 각이 두 바퀴 돌면 이와 같이 부정적분을 구간에 따라 나누어 이어붙여줘야 미적분학의 기본 정리가 성립하게 된다는 것이다. 어차피 z-plane에서 폐경로에 대한 적분은 첫 점과 끝 점이 같으므로, 그 부정적분에 해당하는 함수의 mapping결과(관습적으로 w-plane에서)는 무조건 $2\pi$의 정수배만큼의 각도를 원점을 중심으로 돌게 되고 적분값도 $2\pi$의 정수배가 된다. 지금까지는 피적분함수의 부정적분이 적분경로를 mapping했을 때 한 바퀴도 채 돌지 않은 경우를 다루었다면 앞으로는 2, 3, 4, ...바퀴를 도는 경우를 살펴볼 것이다.

이것에 대한 명확한 수학적 논의를 위해 meromorphic이라는 개념을 도입하자. f가 essential singularity를 가지지 않으면 meromorphic이라 한다. 

DEF 5-1 : meromorphic $\Leftrightarrow$ not having essential singualrity

analytic이면 meromorphic이다. 유리함수 $P(x)/Q(x)$도 $\mathbb{C}$ 전체에서 meromorphic이다. 예를 조금 더 들자면, $\ln z$는 $z=0$에서 essential singularity이므로 not meromorphic이며, $\sin \frac{1}{z}$도 $z=0$이 set of pole의 acc pt이므로 (혹은 essential singularity라서) not meromorphic이다.

THM 5-3 : Argument Principle

$f(z)$ is meromorphic in simple-connected $D$, $C\in D$ is a simple-closed loop and $f(z)$ has neither a pole nor a zero $\forall z \in C$. If $f(z)$ contains $Z$ zeros and $P$ poles inside $C$, then

$$\int_C \frac{f'(z)}{f(z)}dz = i2\pi (Z-P)$$

간단히 이것을 유수정리로 증명해보자. zero를 $a_i (i=1,2,\cdots,Z)$ pole을 $z=b_j (j=1,2,\cdots,P)$라 하자. 그럼 $f(z)$는 zero나 pole이 없는 $g(z)$로 다음과 같이 표현된다.
$$f(z)=\frac{\prod_i (z-a_i)}{\prod_j (z-b_j)}g(z)$$
계산을 열심히 수행하면
$$\frac{f'(z)}{f(z)}=\sum_i\frac{1}{z-a_i} - \sum_j \frac{1}{z-b_i}+\frac{g'(z)}{g(z)}$$
따라서 유수정리에 의해 위의 정리가 증명된다.

방금전의 논리에 의하면 $\frac{f'(z)}{f(z)}$의 한 부정적분은 $\ln |f(z)|+i \arg(f(z))$인데, 이것이 일반적으로 미적분학의 기본정리를 만족시키지 않으며, 아래 그림은 z-plane에서 궤적이 mapping된 $w=f(z)$의 w-plane에서 미적분학의 기본정리를 만족시키게 만들기 위해 w-plane을 이어붙여 나선형으로 만든 후 z-plane의 경로 C가 w-surface에 대응되는 모양을 그린 것이다. 궤적 C가 사상 $w=f(z)$에 대해서 어떻게 대응되는지 살펴보면 왜 각도성분만 살아남는지 알 수 있다. (아래 그림의 경우 2바퀴 도는 경우에 해당함. 이 경우 $Z-P=2$일 것이다.)

이미지 출처 : 위키에서 긁어온 후 편집

즉 우리는 $\int_C \frac{f'(z)}{f(z)}dz$와 같은 꼴의 적분에 한해서 그저 w-plane에서 $f(z)$의 궤적이 원점을 몇 바퀴 도는지만 알아내면 적분을 쉽게 구한다는 것이다. 다음의 예시를 보자.

Q 5-8 : Evaluate $\int_{C_2(0)} \frac{2z+1}{z^2+z} dz$. (문제 출처 : J. H. Mathews & R. W. Howell, Complex Analysis for mathematics and engineering)

A 5-8 : Residue Thm을 이용해도 $i4\pi$를 얻지만 z-plane에서 $C_2(0)$을 $w=f(z)=z^2+z$에 대해 mapping한 것이 원점을 몇 바퀴 도는지 살펴보자.

w-plane에서 간단하게 원점을 기준으로 두 바퀴 도는 것을 확인할 수 있다. 따라서 적분값은 $i2\pi$의 2배이다. THM 5-3도 이 영역에서 zero가 두 개임을 보여준다.

$f(z)+C$의 미분도 $f'(z)$이므로, 꼭 원점을 기준으로 회전수를 잡을 필요 없이 평행이동 시킬 수 있다. 궤적 C의 mapping $w=f(z)$의 $w=w_0$에 대한 회전수를 $Rot(f(C),w_0)$이라 하면 다음의 식이 성립한다. (trivially)
$$\int_C \frac{f'(z)}{f(z)-w_0} dz = i2\pi \, Rot(f(C),w_0) = i2\pi (Z-P)$$
이것을 보통 활용하기를 pole이 없거나 zero가 없는 함수의 zero / pole을 알지 못해도 그것이 궤적의 영점/극점이 내부인지 외부인지를 결정해준다. 다음의 정리를 보자.

THM 5-4 : Rouche's thm

$f$, $g$ are meromorphic in simple-connected $D$, $C \in D$ is closed-loop and $f$, $g$ have neither a pole nor a zero $\forall z \in C$. If $\forall z \in C$, $|f(z)+g(z)|<|f(z)|+|g(z)|$, then $Z_f-P_f=Z_g-P_g$.

$g$가 $C$에서 영점을 갖지 않으므로 $\forall z \in C$에 대하여 $|f/g+1|<|f/g|+1$이 성립한다. 만약 $f/g$가 어떤 점에서 0 또는 양의 실수가 된다면 이 부등식을 위배하는 것이 되므로 $f/g$는 0이나 양의 실수가 될 수 없다. 즉 이것은 $C$의 mapping $f(C)$는 $[0,\infty]$를 지나지 않는다. $w(z)=\ln (f(z)/g(z))$로 두고 미분하면,
$$w(z)=\ln\frac{f(z)}{g(z)}=\ln \left| \frac{f(z)}{g(z)} \right| +i \arg_{(branch=0)} \frac{f(z)}{g(z)} \\ w'(z)=\frac{f'(z)}{f(z)}-\frac{g'(z)}{g(z)}$$
이므로 $w(z)$는 $\frac{f'(z)}{f(z)}-\frac{g'(z)}{g(z)}$의 원시함수이고, THM 5-3에 의해 증명이 끝난다. 예시로 영점이 적분궤적의 내부인지를 판별하는 문제를 보자.

Q 5-9 : $z^4-7z-1=0$의 해 중 $C_1(0)$에 몇 개의 해를 가지는가? (문제 출처 : J. H. Mathews & R. W. Howell, Complex Analysis for mathematics and engineering)

A 5-9 : $f(z)=z^4-7z-1$, $g(z)=7z+1$이라 하자. $z\in C_1(0)$에 대해 $|f+g|=|z|^4=1$이고, $|f(z)|+|g(z)| \geq |g(z)| = |7z+1|\geq 7-1 = 6$이므로 $|f+g|<|f|+|g|$가 성립한다. pole은 존재하지 않으므로 $Z_f=Z_g=1$이다.

복소평면에서의 대수학 기본정리를 Rouche 정리로 증명할 수 있다.

Q 5-10 : 대수학의 기본정리를 증명하라. ($\sum_{k=0}^{n} a_k z^k = 0$의 해는 n개 임을 보여라.)

A 5-10 : $f(z)=-a_n z^n$, $g(z)=\sum_{k=0}^{n} a_k z^k$라 하자. $z \in C_R (0)$, $R>1$ 에 대하여
$$\left| \frac{f(z)+g(z)}{f(z)} \right| = \left| \frac{a_{n-1}}{a_n z^1} + \cdots + \frac{a_0}{a_n z^n} \right| \leq \left| \frac{a_{n-1}}{a_n} \right| \frac{1}{R} +\cdots + \left| \frac{a_0}{a_n} \right| \frac{1}{R^n} < \frac{|a_0|+|a_1|+\cdots+|a_{n-1}|}{|a_n|R}$$
우리는 $R$을 무한정 크게 만들 수 있고, 이 값을 당연히 1보다 작게 만들 수 있다. $f(z)$는 $z=0$에서 n-degenerate zero라서 $Z_f=n$이다. $R \to \infty$이면 $C_R(0)$의 내부는 $\mathbb{C}$이므로 $z \in \mathbb{C}$에 대하여 다음이 성립한다.
$$\left| \frac{f(z)+g(z)}{f(z)} \right| < 1, \:\:\: \left| f(z)+g(z) \right| < |f(z)| \leq |f(z)| + |g(z)|$$
따라서 Rouche's thm에 의해 $\mathbb{C}$에서 해는 n개이다.($Z_g=Z_f=n$)

Rouche thm을 활용하는 문제 중 다소 어려워서 고생했던 문제를 소개한다.

Q 5-11 : 어떤 복소수 $a$가 $|a|>5/2$이다. power series로 정의된 다음의 함수
$$F(z)=\sum_{n=0}^{\infty} \frac{z^n}{a^{n^2}}$$
가 entire analytic이고, $n=1,2,\cdots$에 대하여 다음의 annulus(원환)의 경계에서 0이 아니며, 내부에서 정확히 하나씩의 영점을 가짐을 보여라.
$$|a^{2n-2}| < |z| < |a^{2n}|$$

A 5-11 : 먼저 해당 급수의 수렴성을 살펴보면
$$\liminf_{n\to\infty} \sqrt[n]{|a^{n^2}|}=\liminf_{n\to\infty} |a^n| = \infty$$
이므로 $F(z)$는 $\mathbb{C}$전체에서 수렴한다. 따라서 $F$는 entire function임. $|z|=|a^{2n}|$일 때, 다음을 만족한다고 생각해보자.
$$\left| \frac{z^n}{a^{n^2}} \right| > \left| F(z)-\frac{z^n}{a^{n^2}} \right|$$
이것을 만족하면, $|F(z)|\geq \left| \frac{z^n}{a^{n^2}} \right|- \left| F(z)-\frac{z^n}{a^{n^2}} \right| >0$이므로 annulus의 경계에서 해가 없고, Rouche thm에 의해 annulus 내부에 해가 존재할 것이다. 이제 위의 식을 증명하면 충분하다.
$$\left| F(z)-\frac{z^n}{a^{n^2}} \right|=\left| \sum_{k=0}^{n-1}\frac{z^k}{a^{k^2}}+\sum_{k=n+1}^{\infty}\frac{z^k}{a^{k^2}} \right| \leq \sum_{k=0}^{n-1} |a|^{2nk-k^2}+\sum_{k=n+1}^{\infty}|a|^{2nk-k^2} \\ \leq \sum_{k=0}^{n-1} |a|^{n^2-3n+2+3k}+\sum_{k=n+1}^{\infty}|a|^{n^2+3n+2-3k} \leq \frac{|a|^{n^2-1}}{1-|a|^{-3}}+\frac{|a|^{n^2-1}}{1-|a|^{-3}} < |a|^{n^2}=\left| \frac{z^n}{a^{n^2}} \right|$$
증명끝.