| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Quantum Field Theory
- higher derivatives
- pedagogy
- electromotive force
- Orbital Dynamics
- Taylor expansion
- Rigid Body Dynamics
- Paulo Freire
- 프레이리
- induced emf
- Dirichlet problem
- Tensor Calculus
- Quantum Mechanics
- spinor QED
- Covariant derivatives
- bayesian
- scalar QED
- Electromagnetics
- Pen Art
- Lagrangian Mechanics
- General Relativity
- Noether's thm
- Quantum electodynamics
- RG flow
- Classical Mechanics
- Hamiltonian Mechanics
- Conformal Mapping
- Complex analysis
- Theories of Education
- Topological Tensor
- Today
- Total
목록Quantum Mechanics (2)
Physvillain
In classical physics, all physical quantities were considered to satisfy the commutation relation. For example, in classical mechanics, two quantities $A(x,p)$ and $B(x,p)$ have the commutative property of multiplication. But in the quantum mechanics, the commutation of $A$ and $B$ is not zero in general. \begin{equation}\tag{1} \left[ A(x, p), B(x, p) \right] \neq 0. \end{equation} The history ..
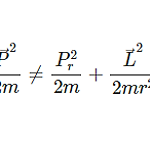 N-dimensional radial momentum operator (TBC)
N-dimensional radial momentum operator (TBC)
이 글은 2019.12.14에 작성되어 아직까지 TBC임. 원본 : physvillain.blogspot.com/2019/12/n-dimensional-radial-momentum-operator.html free particle의 Hamiltonian operator을 생각하자. $$H=-\frac{\hbar^2}{2m}\vec{\nabla}^2$$3차원 spherical coordinate에서 이것은 다음과 같이 써진다. $$H=-\frac{\hbar^2}{2m}\left( \frac{1}{r^2}\partial_r r^2 \partial_r \right)+\frac{\vec{L}^2}{2mr^2}$$그런데 $\frac{1}{r^2} \partial_r r^2 \partial_r = \frac{1}{..
