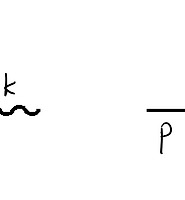| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Conformal Mapping
- Orbital Dynamics
- Tensor Calculus
- RG flow
- Hamiltonian Mechanics
- higher derivatives
- Noether's thm
- Quantum electodynamics
- Taylor expansion
- spinor QED
- electromotive force
- Quantum Field Theory
- Electromagnetics
- 프레이리
- Classical Mechanics
- Complex analysis
- Topological Tensor
- Quantum Mechanics
- scalar QED
- Pen Art
- pedagogy
- induced emf
- bayesian
- Covariant derivatives
- Lagrangian Mechanics
- Paulo Freire
- Theories of Education
- General Relativity
- Rigid Body Dynamics
- Dirichlet problem
- Today
- Total
Physvillain
QFT 1, 2 수강평 본문
1. 배경
지난 해 이론물리학 전공으로서의 꿈을 조금 현실적이고 복잡한 문제로 인해 포기하면서 대전의 모 과기원 물리학과의 양자장및끈이론 연구실을 나오게 되었다.
그렇게 나는 물리교육을 전공으로, 오늘날 이렇게 관악에서 석사과정으로 교직이수를 하여 장래에 교사로서의 커리어를 쌓을 것을 기대하며 공부하고 있다.
2. 동기
현재의 생활에 더할 나위 없이 만족하면서도, 한편으로 작년도에 한참 재밌게 공부하던 QFT를 다시 한 번, 이번에는 좀 더 formal하게 배우고 싶다는 욕심이 생기게 되었다.
당시에는 되게 짧은 시간 내에 압박된 환경 속에서 공부하느라 일단은 이해를 포기한 것들이 많았고, field theory라는 것부터 컨셉 자체가 너무나도 손에 잡히지 않는 느낌이었다.
3. 지향점
나는 감각적인 동물이다.
때문에 내 인식 체계를 벗어난 추상화된 수식들은 생각보다 나를 괴롭게 한다.
의미를 음미하지 않은 채 수학만으로 문제는 풀 수 있겠지만, 그것이 나에게 불편하지 않은 이해를 가져다 주지는 않는다.
비록 나는 다른 사람들보다 주어진 문제를 어떻게든 수학이라는 언어를 사용해서 풀어내는 데에는 많이 뛰어나다고 생각하지만, 정작 성적을 잘 받고 문제를 잘 풀어도 그 안의 의미를 설명하라고 하면 나는 일단 말문이 막힐 수밖에 없다.
field theory가 나에게는 너무나도 감각적으로 와닿지가 않기 때문에, 하물며 이를 양자화한다는 것은 더욱더 그러하기 때문에 조금 더 공부해보고 싶다는 생각이 들었다.
구체적으로 다른 이유들도 많이 있었으나, 아무튼 가장 큰 이유를 꼽자면 장(field)이라는 개념을 조금 시각적으로 와닿게 된다면 우리 물질세계와 조금 더 관련지을 수 있지 않을까 하는 생각일 것이다.
어찌보면 관념세계와 물질세계의 다리를 놓는 일이 아닐까.
예를 들면 스피너라는 것울 설명함에 있어서 다음과 같은 도입부를 생각해보자. (물리천문학부 김현철 선생님께서 제공해주신 설명임)
- 물리학 방정식을 기술하는데 필요한 "재료"는 3개 뿐이다 : 물리량 / derivative / numerical tensor.
- 예컨대, 전자기 Gauss' law에는 kronecker-delta가 들어가고, Empere's law에는 levi-civita가 들어간다 (both numerical tensors).
- 마찬가지로, Schrodinger eq, Klein-Gordon eq에도 numerical tensor가 들어간다.
- 그러나, 안타깝게도, N차원 공간에서 가능한 numerical tensor는 2개 뿐이다 (metric / levi-civita).
- 따라서, 우리는 internal space를 도입해야 한다.
- internal space에서의 numerical tensor 중에서 가장 간단한 것은, 파울리 행렬이다.
이처럼 철저히 논리적인 사고과정은, 비록 엄밀하지만 직관적이지 못하다.
나는 이런 것들을 어쩌면 머리로 '이해'하기보다, 머릿속에 '그려내는' 것을 하고 싶었던 것이다.
단순 기억은 인출의 노력이 없으면 잊혀진다.
논리가 곁들여진 기억은 잊혀지지만 재생산할 수 있다.
그러나 감각이 곁들여진 기억은 생생하게 남는다.
이것이 내가 '감각적인 이해'를 추구하는 궁극적인 이유이다.
애석하게도 나는 천재가 아니고, 두 학기의 수업이 끝나고도 적절히 머리로 그려내지 못했지만, 수업 막바지에 배웠던 Feynman diagram만큼은 놀랍게도 감각적인 느낌이 머릿속을 관통하는 것 같았다.
계산을 symbolize할 뿐만 아니라, 실제로 계산의 노동도 직관의 영역에서 줄여준다는 것은 실로 놀랍다.
4. 교수님에 관해
이준규 교수님은 대한민국 이론물리학 1.5세대즘 되시는 것 같다.
그 분의 제자이신 모 교수님이 하신 말씀이, 누군가 그 분 연구실에 몰래 들어가서 이분 쓰신 강의록을 빼돌려 출판하면 한국 물리학계가 비약적으로 발전할 거라고 한다.
실제로 나는 살면서 강의 준비를 이토록 열심히 하시는 교수님을 만나본 적이 없다. (아마도 이것이 명예교수이시기에 가능한 것일 수도 있다.)연휴에도 휴일에도 얄짤없이 강의가 올라옴은 물론이고, 그마저도 부족해 보강을 많이 하셨....
강의록을 일일이 서필로 작성하심은 물론, 과제도 직접 다 내시고, 때론 어디서든 찾아볼 수 없는 참신한 문제도 만들어 내신다.
문제를 풀다보면 둘 중 하나이다.
- 아 이건 내가 겁나 시간 투자하면 어떻게든 풀 것 같은데?
- 아 이건 진짜 감도 안 오는데?
생각보다 나는 후자였던 문제도 어떻게든 풀어낸 것도 꽤 있는데, 아무렴 이건 그냥 수학문제를 풀듯 해서 그런 것일지도 모른다.
후자에 해당하는 문제는 가지고 있는 QFT 텍스트나 간혹 구글 서칭으로 해결한 것도 있다.
완전히 똑같진 않더라도, 대략적인 감을 잡을 수도 있다.

시간만 투자하면 어떻게든 해결 될 것 같은 문제들 중 일부는 상당히 뻐킹한 계산양을 자랑했는데, 몇몇 이런 문제들은 다른 수강생들이 생각보다 시간 투자를 할 수 없는 상황에 있었기에, 상대적으로 점수를 잘 받을 수 있었던 것 같다. (그냥 할 짓 없을 때 계산하다보면 시간 잘 가더라.)
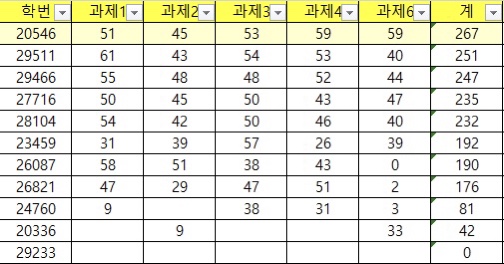
점수 분포를 보아하니, 고인물만 남아버린 것이 틀림 없다.
정말로...
'Quantum Field Theory' 카테고리의 다른 글
| Divergences and Dimensional Regularization of QED (continued) (0) | 2022.01.06 |
|---|---|
| Divergences and Dimensional Regularization of QED (0) | 2022.01.01 |
| Quantum Field Theory II, Problem set 6, 2021 (0) | 2021.12.21 |
| Quantum Field Theory II, Problem set 4, 2021 (0) | 2021.11.22 |
| Quantum Field Theory II, Problem set 3, 2021 (1) | 2021.11.06 |