| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Covariant derivatives
- Quantum Field Theory
- pedagogy
- Conformal Mapping
- 프레이리
- Classical Mechanics
- Quantum electodynamics
- Paulo Freire
- Orbital Dynamics
- scalar QED
- spinor QED
- induced emf
- RG flow
- Dirichlet problem
- Pen Art
- Taylor expansion
- bayesian
- electromotive force
- Tensor Calculus
- Electromagnetics
- Rigid Body Dynamics
- Topological Tensor
- Quantum Mechanics
- Lagrangian Mechanics
- Theories of Education
- Noether's thm
- higher derivatives
- Complex analysis
- Hamiltonian Mechanics
- General Relativity
- Today
- Total
Physvillain
Divergences and Dimensional Regularization of QED (continued) 본문
Divergences and Dimensional Regularization of QED (continued)
Physvillain 2022. 1. 6. 21:38
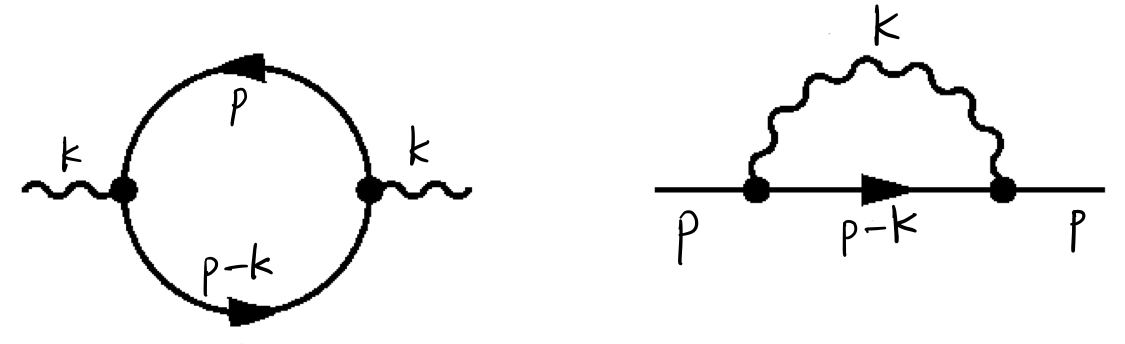
Next, we calculate the vacuum polarization graph. The Feynman rules give
$$i\Pi^{\mu\nu}(k) = -(-ie)^2 \int \frac{d^4 p}{(2\pi)^4} \mathrm{Tr} \left( \gamma^\mu \frac{i}{\not\! p - m} \gamma^\nu \frac{i}{\not \! p - \not \! k - m}\right)$$
In $d$ dimensions,
$$\begin{align} \Pi_{\mu\nu}(k) & = i\mu^{4-d} e^2 \int \frac{d^d p}{(2\pi)^d} \mathrm{Tr} \left( \gamma_\mu \frac{i}{\not\! p - m} \gamma_\nu \frac{i}{\not \! p - \not \! k - m}\right) \\ & = ie^2 \mu^{4-d} \int \frac{d^d p}{(2\pi)^d} \frac{\mathrm{Tr} [\gamma_\mu (\not\! p + m)\gamma_\nu (\not\! p -\not \! k + m)]}{(p^2-m^2)[(p-k)^2-m^2]} \end{align}$$
Introducing Feynman parameter, and putting $p'=p-kz$ then gives
$$\Pi_{\mu\nu}(k) = ie^2 \mu^{4-d} \int_0^1 dz \int \frac{d^d p'}{(2\pi)^d} \frac{\mathrm{Tr}[\gamma_\mu (\not\! p' + \not\! k z+m)\gamma_\nu (\not\! p' -\not\! k(1-z) + m)]}{[{p'}^2-m^2+k^2 z(1-z)]^2}$$
Since the trace of odd gamma's vanishes, and because the terms odd in $p'$ give no contribution to the integral, the numerator in the momentum space is
$$\text{(numerator)} = \left[ {p'}^\kappa {p'}^\lambda - k^\kappa k^\lambda z(1-z) \right] \mathrm{Tr}(\gamma_\mu \gamma_\kappa \gamma_\nu \gamma_\lambda) + m^2 \mathrm{Tr}(\gamma_\mu \gamma_\nu)$$
which gives, from $\mathrm{Tr} I = f(d), \; \mathrm{Tr} \gamma_\mu \gamma_\nu = f(d) g_{\mu\nu}, \;\; \mathrm{Tr} \gamma_\mu \gamma_\kappa \gamma_\nu \gamma_\lambda = f(d) (g_{\mu\kappa} g_{\nu\lambda} - g_{\mu\nu} g_{\kappa\lambda}+g_{\mu\lambda}g_{\kappa\nu})$,
$$\text{(numerator)} = f(d) \left\{ 2{p'}_\mu {p'}_\nu - 2z(1-z)(k_\mu k_\nu - k^2 g_{\mu\nu}) - g_{\mu\nu}\left[ {p'}^2 -m^2 + k^2 z(1-z) \right] \right\}$$
Hence putting $p' \to p$,
$$\Pi_{\mu\nu}(k) = ie^2 \mu^{4-d} \int_0^1 dz \int \frac{d^d p}{(2\pi)^d} \left\{ \frac{2p_\mu p_\nu}{[p^2-m^2+k^2 z(1-z)]^2} - \frac{2z(1-z)(k_\mu k_\nu - g_{\mu\nu}k^2)}{[p^2 -m^2 + k^2 z(1-z)]} - \frac{g_{\mu\nu}}{[p^2-m^2 + k^2 z(1-z)]} \right\}$$
From eqs $(2)$ and $(4)$ (introduced and derived in the previous post) :
$$\int \frac{d^d p}{(p^2+2pq-m^2)^\alpha} = (-1)^{d/2} i \pi^{d/2} \frac{\Gamma\left( \alpha -d/2 \right)}{\Gamma(\alpha)}\frac{1}{[-q^2-m^2]^{\alpha-d/2}} \;\;\;\;\;\;\;\;\;\;\;\;\;\; (2)$$
$$\int d^d p \frac{p^2}{(p^2+2pq-m^2)^\alpha} = (-1)^{d/2} \frac{i \pi^{d/2}}{\Gamma(\alpha) (-q^2-m^2)^{\alpha-d/2}} \left[ q^2 \Gamma\left( \alpha - \frac{d}{2} \right) + \frac{d}{2} (-q^2-m^2) \Gamma\left( \alpha-1-\frac{d}{2} \right) \right] \;\;\;\;\;\; (4)$$
the contributions of the first and third terms in the integrand cancel. The middle term leads to a logarithmically divergent integral (same as the photon loop case), whose value is obtained from $(2)$.
$$\Pi_{\mu\nu}(k) = \frac{e^2}{2\pi^2} (k_\mu k_\nu - g_{\mu\nu} k^2) \left\{ \frac{1}{3\epsilon} - \frac{\gamma}{6} - \int_0^1 dz z(1-z) \ln \left[ \frac{-m^2 + k^2 z(1-z)}{4\pi\mu^2} \right] + \mathcal{O}(\epsilon) \right\}$$
As expected, the divergent part is a pole in $\epsilon$. The finite part contains terms depending on $k^2$, so for small $k^2$ we have
$$\Pi_{\mu\nu}(k) = \frac{e^2}{6\pi^2} (k_\mu k_\nu - g_{\mu\nu} k^2) \left( \frac{1}{\epsilon} + \frac{k^2}{10m^2} + \cdots \right) = \frac{e^2}{6\pi \epsilon} (k_\mu k_\nu - g_{\mu\nu} k^2) + \text{finite}$$
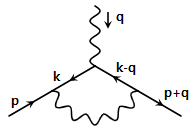
Now we evaluate the vertex diagram of Fig 3. Feynman rules give
$$-ie\Lambda_\mu (p, q, p+q) = (-ie)^3 \int \frac{d^4 k}{(2\pi)^4} \frac{-ig_{\rho\sigma}}{(k+p)^2} \gamma^\rho \frac{i}{\not\! k - \not\! q -m} \gamma_\mu \frac{i}{\not\! k -m} \gamma^\sigma$$
This gives
$$\begin{align} -ie\Lambda_\mu (p, q, p') &= \left(-ie \mu^{2-d/2}\right)^3 \int \frac{d^d k}{(2\pi)^d} \gamma_\nu \frac{i}{\not\! p' -\not\! k - m} \gamma_\mu \frac{i}{\not\! p -\not\! k -m} \gamma_\rho \frac{-ig^{\nu\rho}}{k^2} \\ & = -\left(e \mu^{2-d/2}\right)^3 \int \frac{d^d k}{(2\pi)^d} \frac{\gamma_\nu (\not\! p' - \not\! k +m) \gamma_\mu (\not\! p -\not\! k + m) \gamma^\nu}{k^2 [(p-k)^2 - m^2] [(p'-k)^2 - m^2]} \end{align}$$
Now introducing the 2-parameter Feynman formula :
$$\frac{1}{abc} = 2 \int_0^1 dx \int_0^{1-x} dy \frac{1}{[a(1-x-y) + bx + cy]^3}$$
which gives
$$\Lambda_\mu (p, q, p') = -\frac{2ie^2 \mu^{4-d}}{(2\pi)^d} \int_0^1 dx \int_0^{1-x}dy \int d^d k \frac{\gamma_\nu (\not\! p' - \not\! k + m) \gamma_\mu (\not\! p - \not\! k + m) \gamma^\nu}{\left[ k^2-m^2(x+y) - 2k(px+p'y) + p^2 x + {p'}^2 y \right]^3}$$
Defining $k'=k-px-p'y$ then gives ($k'\to k$)
$$\Lambda_\mu (p, q, p') = -\frac{2ie^2 \mu^{4-d}}{(2\pi)^d} \int_0^1 dx \int_0^{1-x}dy \int d^d k \frac{\gamma_\nu [\not\! p' (1-y) -\not\! p x - \not\! k +m] \gamma_\mu [\not\! p (1-x) - \not\! p' y -\not\! k + m] \gamma^\nu}{\left[ k^2 -m^2(x+y) + p^2 x(1-x) + {p'}^2 y(1-y) - 2p \cdot p' xy \right]^3}$$
It contains convergent and divergent pieces. The part of the numerator quadratic in $k$ is divergent, the rest convergent, so we can put
$$\Lambda_\mu = \Lambda_\mu^{\text{(div)}} + \Lambda_\mu^{\text{(conv)}}$$
The divergent part may be written, from $(4)$, as
$$\Lambda_\mu^{\text{(div)}} (p, q, p') = \frac{e^2}{2} \mu^{4-d} \left( \frac{1}{4\pi} \right)^{d/2} \Gamma\left(2-\frac{d}{2}\right) \int_0^1 dx \int_0^{1-x} dy \frac{\gamma_\nu \gamma_\rho \gamma_\mu \gamma^\rho \gamma^\nu}{\left[ -m^2 (x+y) + p^2 x(1-x) + {p'}^2 y(1-y) - 2p \cdot p' xy \right]^{2-d/2}}$$
using the 5-gamma identity
$$\gamma_\nu \gamma_\rho \gamma_\mu \gamma_\sigma \gamma^\nu = (2-d) \gamma_\rho \gamma_\mu \gamma_\sigma + 2(\gamma_\mu \gamma_\sigma \gamma_\rho - \gamma_\rho \gamma_\sigma \gamma_\mu)$$
we get
$$\gamma_\nu \gamma_\rho \gamma_\mu \gamma^\rho \gamma^\nu = (2-d)^2 \gamma_\mu$$
Putting $\epsilon = 4-d$, so that $(2-d)^2 = 4-4\epsilon + \mathcal{O}(\epsilon^2)$, we get
$$\Lambda_\mu^{\text{(div)}} (p, q, p') = \frac{e^2}{8\pi^2 \epsilon} \gamma^\mu + \text{finite}$$
The convergent part is that part with no $k$ in the numerator of the integrand. Since it is convergent, we may put $d=4$ and perform the integration over $k$ using $(2)$. Hence we get
$$\Lambda_\mu^{\text{(conv)}} (p, q, p') = \frac{e^2}{16\pi^2} \int_0^1 dx \int_0^{1-x} dy \frac{\gamma_\nu [\not\! p' (1-y) - \not\! p x + m] \gamma_\mu [\not\! p (1-x) -\not\! p' y + m] \gamma^\nu}{m^2 (x+y) - p^2 x(1-x) - {p'}^2 y (1-y) + 2p\cdot p' xy}$$
Now we have explicit expressions for the 3 divergent diagrams in QED, and we have 3 divergent terms and 1 convergent term. These divergent terms may be cancelled by counter-terms in the Lagrangian, which is called 'renormalization'. And we can get, from the convergent term, an anomalous magnetic moment to the electron, which is famously known as 'g-factor' of the electron or a 'gyromagnetic ratio' :
$$\frac{g}{2} = 1+\frac{\alpha}{2\pi} + \mathcal{O}(\alpha^2)$$
'Quantum Field Theory' 카테고리의 다른 글
| Field theoretical origin of mass (1) | 2023.10.19 |
|---|---|
| Today's Physics : 물리학자들이 알려주는 수학으로 사기치는 방법(1) (0) | 2022.04.27 |
| Divergences and Dimensional Regularization of QED (0) | 2022.01.01 |
| QFT 1, 2 수강평 (0) | 2021.12.27 |
| Quantum Field Theory II, Problem set 6, 2021 (0) | 2021.12.21 |